我们知道只是一种特殊的二叉树,大部分二叉树的结点都是不完全存在左右孩子的,即很多指针域没有被充分地利用。另一方面我们在对一棵二叉树做的时候,得到一串字符序列,遍历过后,我们可以知道结点之间的前驱后继关系,也就是说,我们可以很清楚地知道任意一个结点,它的前驱和后继是哪一个。可是这是建立在已经遍历过的基础之上的。在二叉链表上,我们只能知道每个结点指向其左右孩子结点的地址,而不知道某个结点的前驱是谁,后继是谁。要想知道,必须遍历一次。以后每次需要知道时,都必须遍历一次。为什么不考虑在创建时就记住这些前驱和后继呢?那将是多大的时间上的节省。
综合刚才两个角度的分析后,我们可以考虑利用那些空地址,存放指向结点在某次遍历次序下的前驱和后继结点的地址。我们把这种指向前驱和后继的指针称为线索,加上线索的二叉链表称为线索链表,相应的二叉树就称为线索二叉树(Threaded Binary Tree)。
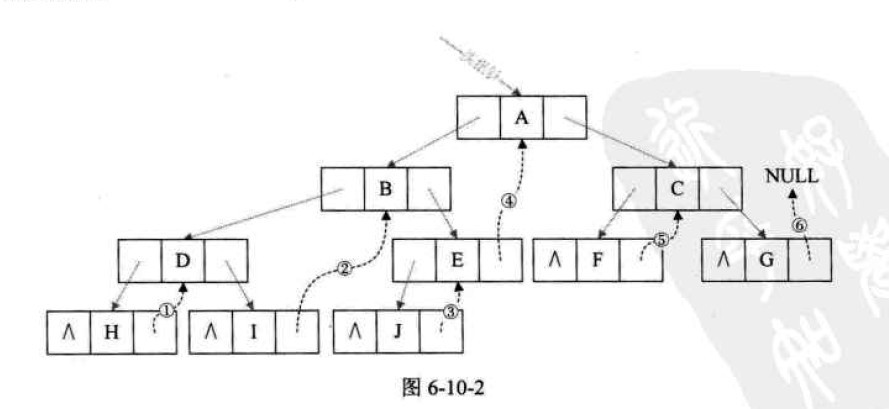
如图6-10-2,我们把这棵二叉树进行中序遍历后,将所有的空指针域中的rchild,改为指向它的后继结点。
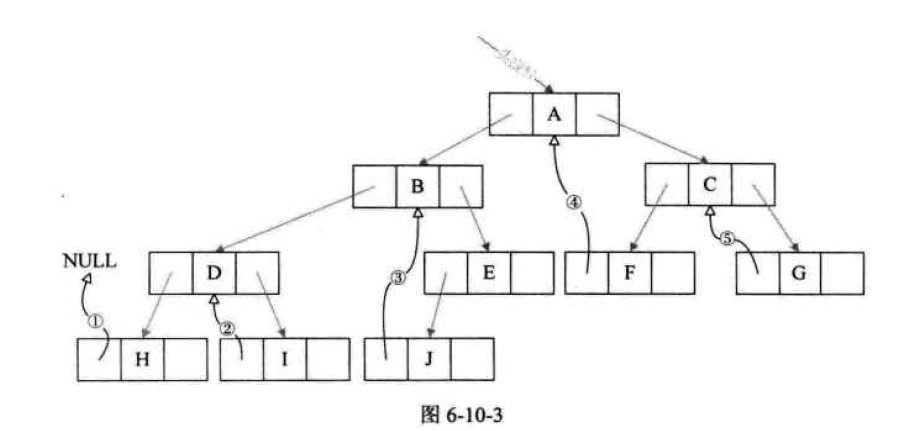
如图6-10-3,我们把这棵二叉树进行中序遍历后,将所有的空指针域中的lchild,改为指向它的前驱结点。
通过图6-10-4(空心箭头实线为前驱,虚线黑箭头为后继),更容易看出,其实线索二叉树,等于是把一棵二叉树转变成了一个双向链表,这样对我们的插入删除结点,查找某个结点都带来了方便。所以我们把对二叉树以某种次序遍历使其变为线索二叉树的过程称做是线索化。
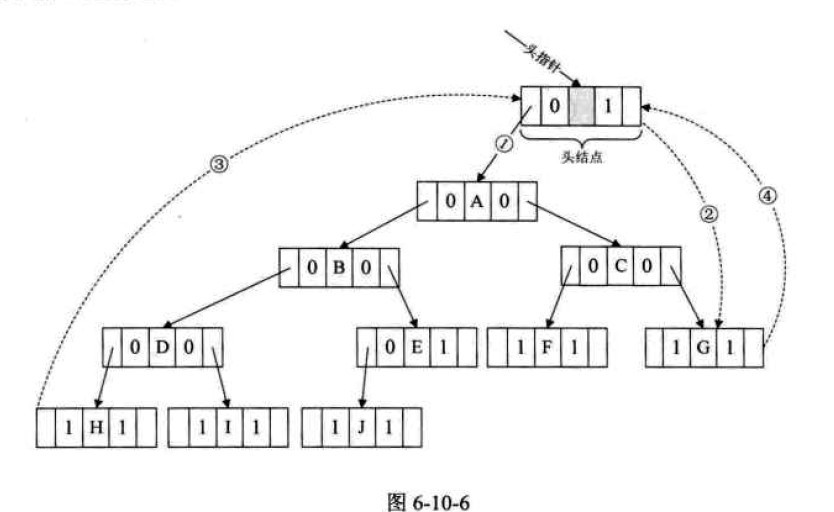
为了区分指针域是指向左右孩子还是前驱后继,需要再增加两个标志位ltag和rtag,ltag为0时表示指向左孩子,为1时表示指向前驱,rtag为0时表示指向右孩子,为1时表示指向后继。和双向链表结构一样,可以在二叉树线索链表上添加一个头结点,如图6-10-6所示,这样做的好处是我们既可以从第一个结点H开始顺后继进行遍历(利用1,4两根线),也可以从最后一个结点G开始顺前驱进行遍历(利用2,3两根线),将头结点作为遍历结束的判据。
示例程序如下:(改编自《大话数据结构》)
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 | #include<iostream>using namespace std;#define MAXSIZE 50typedef char ElemType;typedef enum { Link, Thread } PointerTag;typedef char String[MAXSIZE + 1]; //以'\0’结尾 String str; /* 用于构造二叉树*//* 结点结构 */typedef struct BThrNode { ElemType data;/* 结点数据 */ struct BThrNode *LChild;/* 左右孩子指针 */ struct BThrNode *RChild; PointerTag LTag; PointerTag RTag; } BThrNode, *BThrNodePtr;/* 构造一个字符串 */bool StrAssign(String Dest, char *ptr) { cout << "Assign Str ..." << endl; int i; for (i = 0; ptr[i] != '\0' && i < MAXSIZE; i++) Dest[i] = ptr[i]; Dest[i] = '\0'; return true; }bool CreateBThrTree(BThrNodePtr *Tpp) { ElemType ch; static int i = 0; if (str[i] != '\0') ch = str[i++]; if (ch == '#') *Tpp = NULL; else { *Tpp = (BThrNodePtr)malloc(sizeof(BThrNode)); if (!*Tpp) exit(1); (*Tpp)->data = ch;/* 生成根结点 */ CreateBThrTree(&(*Tpp)->LChild);/* 构造左子树 */ if ((*Tpp)->LChild) (*Tpp)->LTag = Link; CreateBThrTree(&(*Tpp)->RChild);/* 构造右子树 */ if ((*Tpp)->RChild) (*Tpp)->RTag = Link; } return true; } BThrNodePtr prev;/* 全局变量,始终指向刚刚访问过的结点 *//* 中序遍历进行中序线索化 */void InThreading(BThrNodePtr Tp) { if (Tp) { InThreading(Tp->LChild);/* 在第一次左递归过程中绑定了如图的线条3 */ if (!Tp->LChild)/* 没有左孩子 */ { Tp->LTag = Thread;/* 前驱线索 */ Tp->LChild = prev;/* 左孩子指针指向前驱 */ } if (!prev->RChild)/* 前驱没有右孩子 */ { prev->RTag = Thread;/* 后继线索 */ prev->RChild = Tp;/* 前驱右孩子指针指向后继(当前结点Tp) */ } prev = Tp; InThreading(Tp->RChild);/* 递归右子树线索化 */ } }/* 中序遍历二叉树,并将其中序线索化,*Hpp指向头结点 */bool InOrderThreading(BThrNodePtr *Hpp, BThrNodePtr Tp) { cout << "InOrderThreading ..." << endl; *Hpp = (BThrNodePtr)malloc(sizeof(BThrNode)); if (!(*Hpp)) exit(1); (*Hpp)->LTag = Link;/* 建头结点 */ (*Hpp)->RTag = Thread; (*Hpp)->RChild = (*Hpp);/* 右指针回指 */ if (!Tp) (*Hpp)->LChild = *Hpp;/* 若二叉树空,则左指针回指 */ else { (*Hpp)->LChild = Tp; /* 绑定如图的线1 */ prev = (*Hpp); /* 头结点是第一个走过的点*/ InThreading(Tp); /* 中序遍历进行中序线索化 */ prev->RChild = *Hpp; /* 最后一个结点的后继指向头结点,即如图的线4*/ prev->RTag = Thread; (*Hpp)->RChild = prev; /* 头结点的后继指向最后一个结点,即如图的线2*/ } }/* 中序遍历二叉线索树(头结点)的非递归算法 */bool InOrderTraverse_Thr(BThrNodePtr Hp) { cout << "InOrderTraverse ..." << endl; BThrNodePtr Bp; Bp = Hp->LChild;/* Bp指向根结点 */ while (Bp != Hp) { /* 空树或遍历结束时,Bp== Hp */ while (Bp->LTag == Link) Bp = Bp->LChild; /* 访问其左子树为空的结点 */ cout << Bp->data << ' '; while (Bp->RTag == Thread && Bp->RChild != Hp) { Bp = Bp->RChild; cout << Bp->data << ' '; /* 访问后继结点 */ } Bp = Bp->RChild; } return true; }int main(void) { BThrNodePtr Hp, Tp; StrAssign(str, "ABDH##I##EJ###CF##G##"); cout << "输入前序遍历序列 :" << endl; cout << str << endl; CreateBThrTree(&Tp); InOrderThreading(&Hp, Tp); InOrderTraverse_Thr(Hp); return 0; } |
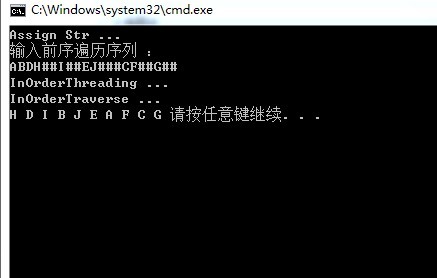
输出为:
由于线索二叉树充分利用了空指针域的空间,又保证了创建时一次遍历就可以持续受用的前驱后继信息,所以如果所用的二叉树需要经常遍历或查找结点时需要某种遍历序列中的前驱后继,那么采用线索二叉链表的存储结构就是不错的选择。